In my skilled life as a knowledge scientist, I’ve encountered time sequence a number of instances. Most of my data comes from my educational expertise, particularly my programs in Econometrics (I’ve a level in Economics), the place we studied statistical properties and fashions of time sequence.
Among the many fashions I studied was SARIMA, which acknowledges the seasonality of a time sequence, nevertheless, we’ve got by no means studied the best way to intercept and acknowledge seasonality patterns.
More often than not I needed to discover seasonal patterns I merely relied on visible inspections of information. This was till I found this YouTube video on Fourier transforms and ultimately discovered what a periodogram is.
On this weblog put up, I’ll clarify and apply easy ideas that can flip into helpful instruments that each DS who’s finding out time sequence ought to know.
Desk of Contents
- What’s a Fourier Remodel?
- Fourier Remodel in Python
- Periodogram
Overview
Let’s assume I’ve the next dataset (AEP energy consumption, CC0 license):
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("information/AEP_hourly.csv", index_col=0)
df.index = pd.to_datetime(df.index)
df.sort_index(inplace=True)
fig, ax = plt.subplots(figsize=(20,4))
df.plot(ax=ax)
plt.tight_layout()
plt.present()It is rather clear, simply from a visible inspection, that seasonal patterns are enjoying a job, nevertheless it could be trivial to intercept all of them.
As defined earlier than, the invention course of I used to carry out was primarily guide, and it might have seemed one thing as follows:
fig, ax = plt.subplots(3, 1, figsize=(20,9))
df_3y = df[(df.index >= '2006–01–01') & (df.index < '2010–01–01')]
df_3M = df[(df.index >= '2006–01–01') & (df.index < '2006–04–01')]
df_7d = df[(df.index >= '2006–01–01') & (df.index < '2006–01–08')]
ax[0].set_title('AEP power consumption 3Y')
df_3y[['AEP_MW']].groupby(pd.Grouper(freq = 'D')).sum().plot(ax=ax[0])
for date in df_3y[[True if x % (24 * 365.25 / 2) == 0 else False for x in range(len(df_3y))]].index.tolist():
ax[0].axvline(date, coloration = 'r', alpha = 0.5)
ax[1].set_title('AEP power consumption 3M')
df_3M[['AEP_MW']].plot(ax=ax[1])
for date in df_3M[[True if x % (24 * 7) == 0 else False for x in range(len(df_3M))]].index.tolist():
ax[1].axvline(date, coloration = 'r', alpha = 0.5)
ax[2].set_title('AEP power consumption 7D')
df_7d[['AEP_MW']].plot(ax=ax[2])
for date in df_7d[[True if x % 24 == 0 else False for x in range(len(df_7d))]].index.tolist():
ax[2].axvline(date, coloration = 'r', alpha = 0.5)
plt.tight_layout()
plt.present()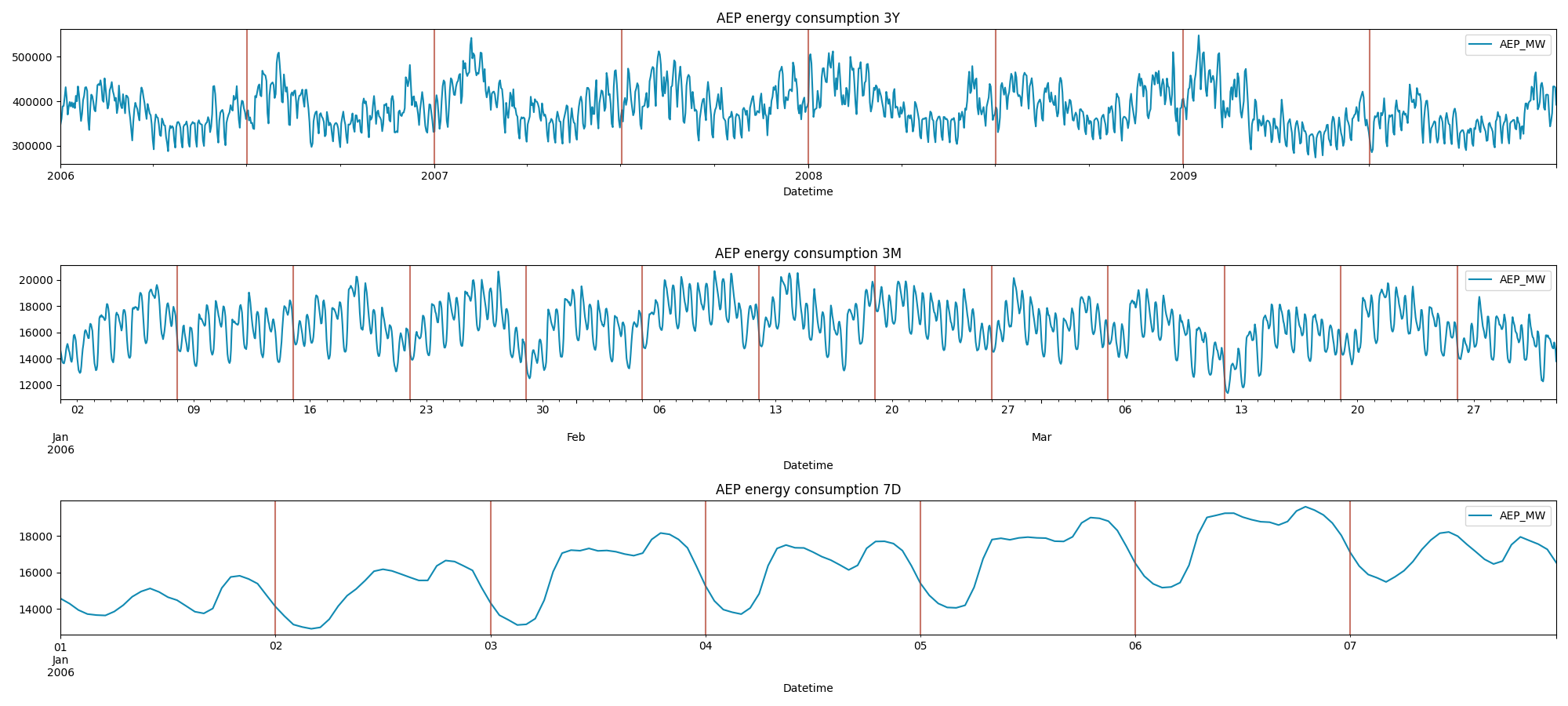
This can be a extra in-depth visualization of this time sequence. As we are able to see the next patterns are influencing the information: **- a 6 month cycle,
- a weekly cycle,
- and a day by day cycle.**
This dataset exhibits power consumption, so these seasonal patterns are simply inferable simply from area data. Nonetheless, by relying solely on a guide inspection we might miss essential informations. These could possibly be among the most important drawbacks:
- Subjectivity: We’d miss much less apparent patterns.
- Time-consuming : We have to take a look at completely different timeframes one after the other.
- Scalability points: Works properly for just a few datasets, however inefficient for large-scale evaluation.
As a Information Scientist it will be helpful to have a instrument that offers us speedy suggestions on crucial frequencies that compose the time sequence. That is the place the Fourier Transforms come to assist.
1. What’s a Fourier Remodel
The Fourier Remodel is a mathematical instrument that permits us to “swap area”.
Often, we visualize our information within the time area. Nonetheless, utilizing a Fourier Remodel, we are able to swap to the frequency area, which exhibits the frequencies which are current within the sign and their relative contribution to the unique time sequence.
Instinct
Any well-behaved operate f(x) might be written as a sum of sinusoids with completely different frequencies, amplitudes and phases. In easy phrases, each sign (time sequence) is only a mixture of easy waveforms.
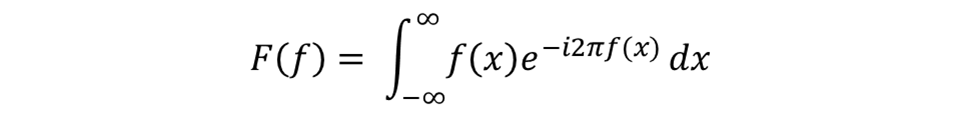
The place:
- F(f) represents the operate within the frequency area.
- f(x) is the unique operate within the time area.
- exp(−i2πf(x)) is a posh exponential that acts as a “frequency filter”.
Thus, F(f) tells us how a lot frequency f is current within the authentic operate.
Instance
Let’s think about a sign composed of three sine waves with frequencies 2 Hz, 3 Hz, and 5 Hz:
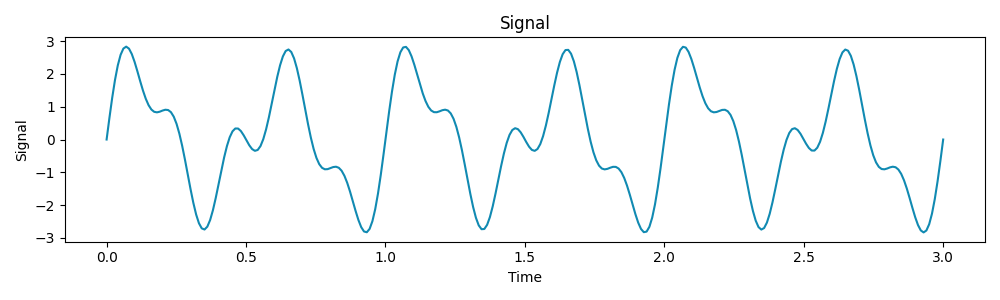
Now, let’s apply a Fourier Remodel to extract these frequencies from the sign:
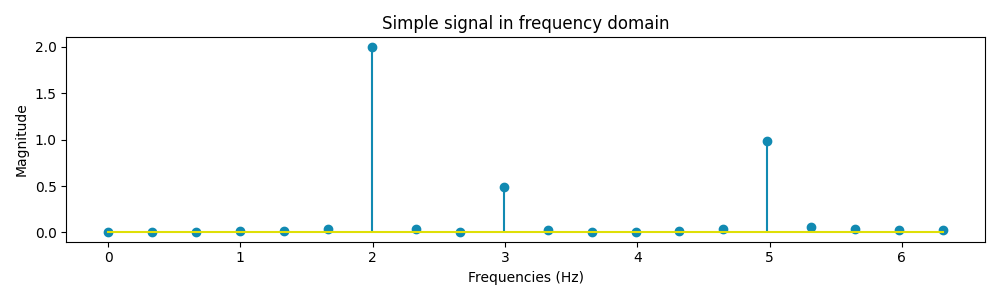
The graph above represents our sign expressed within the frequency area as a substitute of the traditional time area. From the ensuing plot, we are able to see that our sign is decomposed in 3 parts of frequency 2 Hz, 3 Hz and 5 Hz as anticipated from the beginning sign.
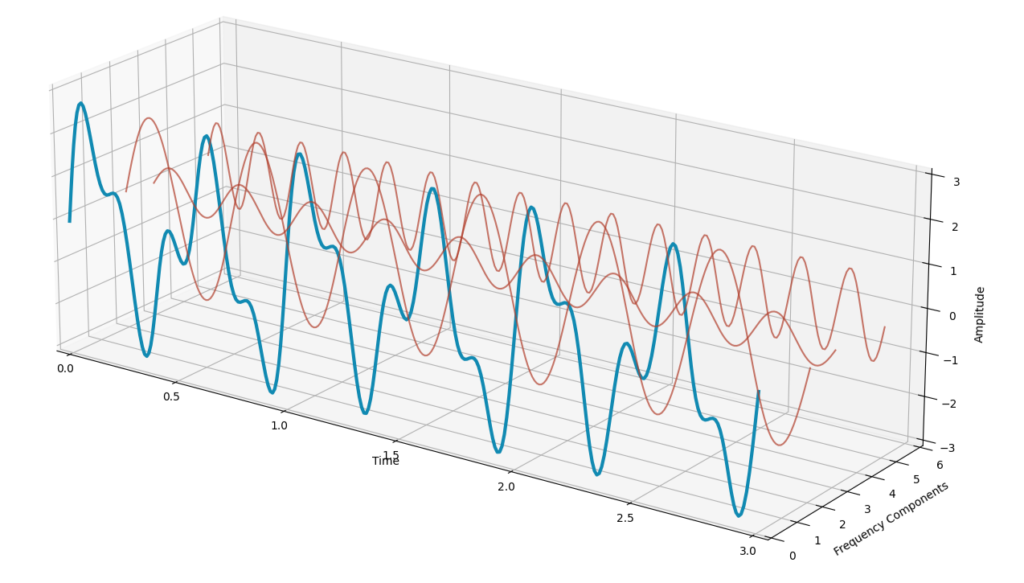
As stated earlier than, any well-behaved operate might be written as a sum of sinusoids. With the data we’ve got to this point it’s potential to decompose our sign into three sinusoids:
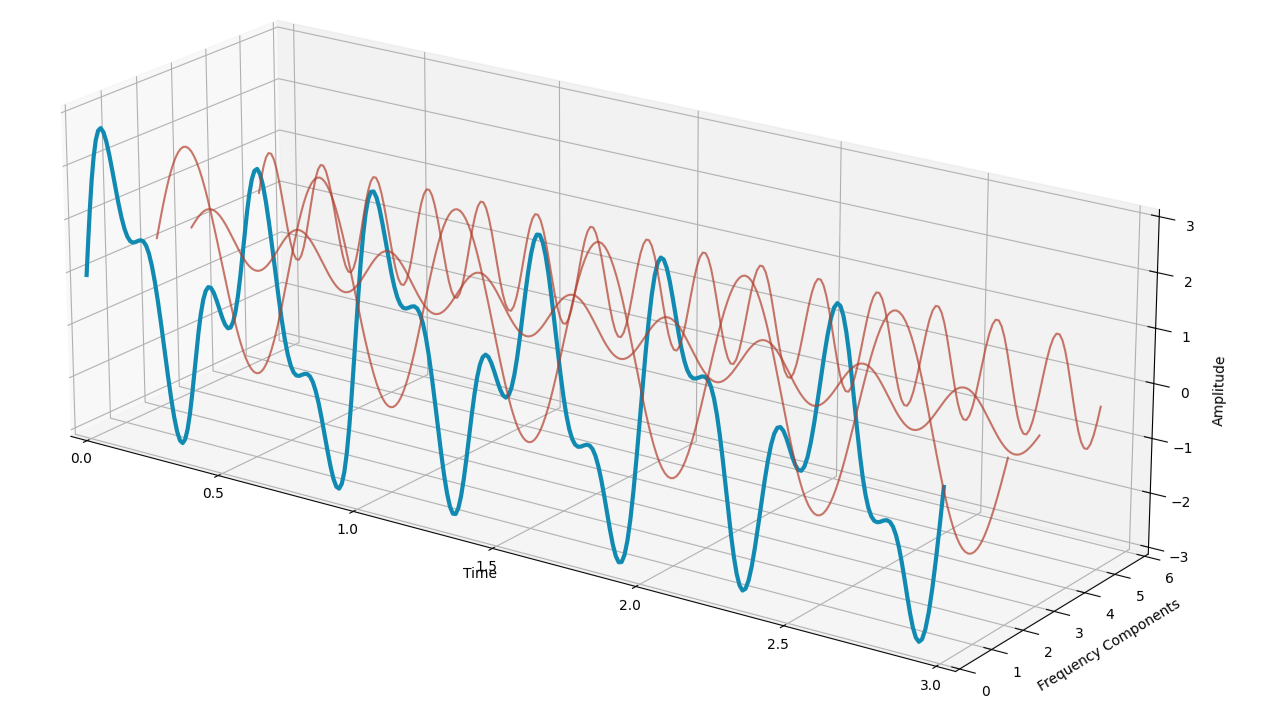
The unique sign (in blue) might be obtained by summing the three waves (in crimson). This course of can simply be utilized in any time sequence to guage the principle frequencies that compose the time sequence.
2 Fourier Remodel in Python
On condition that it’s fairly simple to change between the time area and the frequency area, let’s take a look on the AEP power consumption time sequence we began finding out firstly of the article.
Python supplies the “numpy.fft” library to compute the Fourier Remodel for discrete alerts. FFT stands for Quick Fourier Remodel which is an algorithm used to decompose a discrete sign into its frequency parts:
from numpy import fft
X = fft.fft(df['AEP_MW'])
N = len(X)
frequencies = fft.fftfreq(N, 1)
durations = 1 / frequencies
fft_magnitude = np.abs(X) / N
masks = frequencies >= 0
# Plot the Fourier Remodel
fig, ax = plt.subplots(figsize=(20, 3))
ax.step(durations[mask], fft_magnitude[mask]) # Solely plot optimistic frequencies
ax.set_xscale('log')
ax.xaxis.set_major_formatter('{x:,.0f}')
ax.set_title('AEP power consumption - Frequency-Area')
ax.set_xlabel('Frequency (Hz)')
ax.set_ylabel('Magnitude')
plt.present()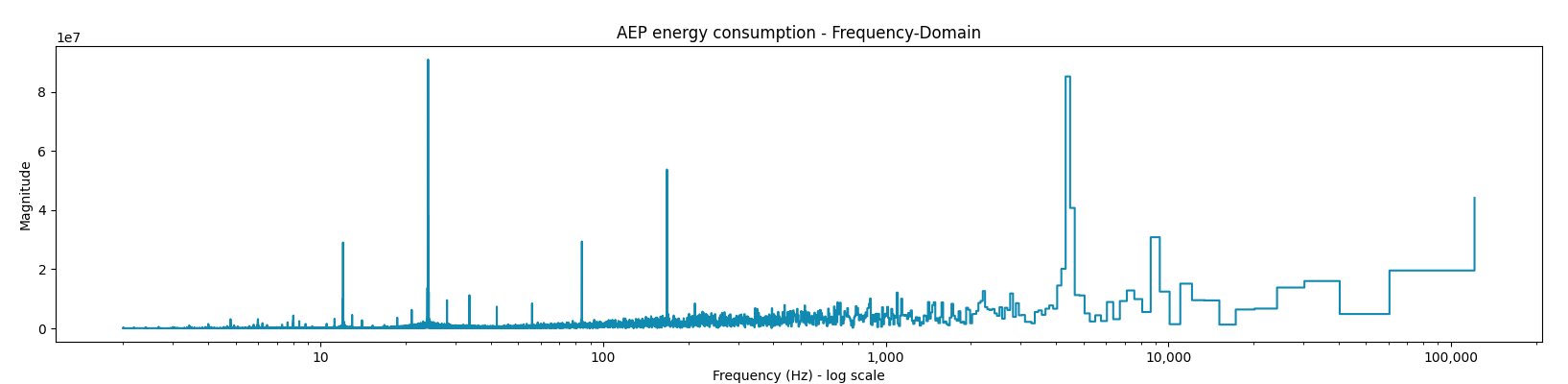
That is the frequency area visualization of the AEP_MW power consumption. Once we analyze the graph we are able to already see that at sure frequencies we’ve got a better magnitude, implying increased significance of such frequencies.
Nonetheless, earlier than doing so we add yet one more piece of idea that can enable us to construct a periodogram, that can give us a greater view of crucial frequencies.
3. Periodogram
The periodogram is a frequency-domain illustration of the energy spectral density (PSD) of a sign. Whereas the Fourier Remodel tells us which frequencies are current in a sign, the periodogram quantifies the facility (or depth) of these frequencies. This passage is usefull because it reduces the noise of much less essential frequencies.
Mathematically, the periodogram is given by:
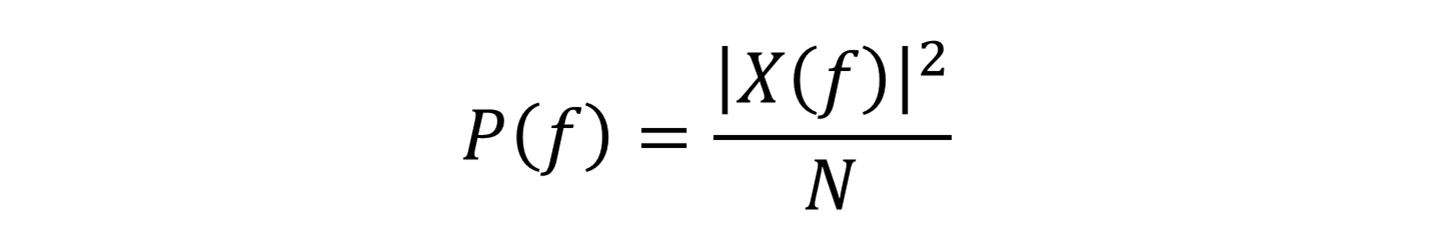
The place:
- P(f) is the facility spectral density (PSD) at frequency f,
- X(f) is the Fourier Remodel of the sign,
- N is the full variety of samples.
This may be achieved in Python as follows:
power_spectrum = np.abs(X)**2 / N # Energy at every frequency
fig, ax = plt.subplots(figsize=(20, 3))
ax.step(durations[mask], power_spectrum[mask])
ax.set_title('AEP power consumption Periodogram')
ax.set_xscale('log')
ax.xaxis.set_major_formatter('{x:,.0f}')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Energy')
plt.present()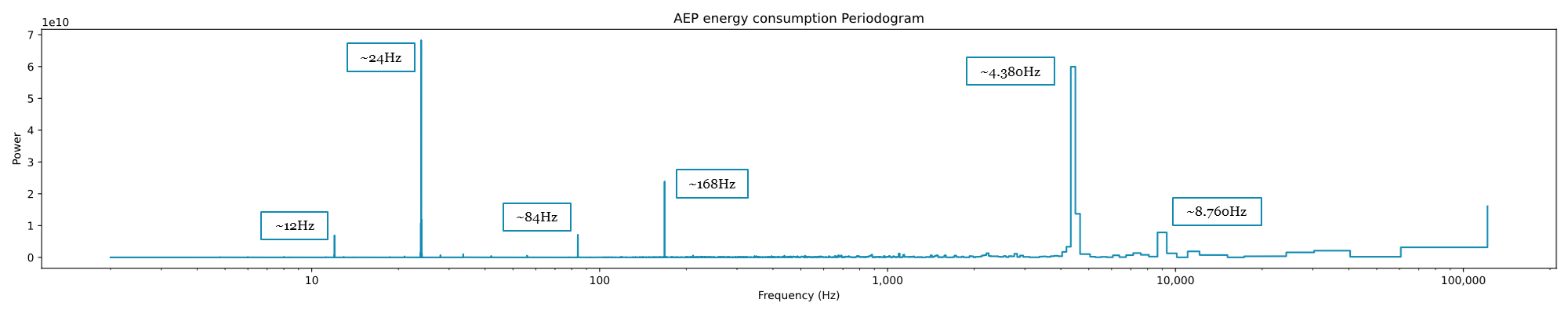
From this periodogram, it’s now potential to draw conclusions. As we are able to see essentially the most highly effective frequencies sit at:
- 24 Hz, equivalent to 24h,
- 4.380 Hz, corresponding to six months,
- and at 168 Hz, equivalent to the weekly cycle.
These three are the identical Seasonality parts we discovered within the guide train performed within the visible inspection. Nonetheless, utilizing this visualization, we are able to see three different cycles, weaker in energy, however current:
- a 12 Hz cycle,
- an 84 Hz cycle, correspondint to half every week,
- an 8.760 Hz cycle, equivalent to a full yr.
It’s also potential to make use of the operate “periodogram” current in scipy to acquire the identical consequence.
from scipy.sign import periodogram
frequencies, power_spectrum = periodogram(df['AEP_MW'], return_onesided=False)
durations = 1 / frequencies
fig, ax = plt.subplots(figsize=(20, 3))
ax.step(durations, power_spectrum)
ax.set_title('Periodogram')
ax.set_xscale('log')
ax.xaxis.set_major_formatter('{x:,.0f}')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Energy')
plt.present()Conclusions
Once we are coping with time sequence some of the essential parts to contemplate is seasonalities.
On this weblog put up, we’ve seen the best way to simply uncover seasonalities inside a time sequence utilizing a periodogram. Offering us with a simple-to-implement instrument that can turn into extraordinarily helpful within the exploratory course of.
Nonetheless, that is simply a place to begin of the potential implementations of Fourier Remodel that we may benefit from, as there are a lot of extra:
- Spectrogram
- Characteristic encoding
- Time sequence decomposition
- …
Please depart some claps when you loved the article and be happy to remark, any suggestion and suggestions is appreciated!
_Here you can find a notebook with the code from this blog post._
Source link